Até agora, foram utilizados apenas erros observados pelas saídas dos neurônios através do ajustes sucessivos dos pesos entre a camada de entrada e a de saída (2 camadas apenas). Mas, se for adicionada mais uma camada intermediaria entre elas, uma camada escondida ?
Bom, de toda maneira ainda é necessário ter o processo de retro-alimentação do erro de volta à rede neural, de forma que possam ser ajustados os pesos. E aí está o problema.

Atualmente, o neurônio ou está "ligado" ou "desligado", o que significa que a sua função de ativação é controlada por um limiar que determina a mudança dos estados do neurônio.
def function(output):
if output >= 0:
return 1
else:
return -1
Plotando o gráfico representando a função acima, pode-se ver as linhas vermelha (representando a sua derivada) e a linha azul (representando a função).
Quaisquer ajustes feitos nos pesos que alimentam a camada escondida com uso desta função terão efeitos não tão eficientes e limitados, devido a sua descontinuidade acentuada . É necessário trocar a função de limiar (threeshold function) por algo melhor, que tenha uma transição mais suave. Pode-se utilizar então, a função sigmóide representada pela equação abaixo:
def sigmoid(output):
return 2/ (1 + math.exp(-2 * output))
E sua derivada:
f'(x) = 1 - f(x)2
def sigmoidDerivative(output):
x = sigmoid(output)
return 1 - (math.pow(x,2))
Pode-se observar que a transição agora entre os valores 1 e -1 é mais suave e contínua e sua derivada tende ao infinito. Esta função é muito popular entre diversos desenvolvedores de redes neurais, porém alguns utilizam uma versão modificada deste. Variando os limites da função de 0 até 1 (em vez de -1 a 1) tem o benefício de ser computacionalmente menos custoso e interessante quando aplicado em redes neurais de grande dimensão.
Para isso, utiliza-se a função:
def sigmoid(output):
return 2/ (1 + math.exp(-output))
E sua derivada:
f'(x) = f(x)(1 - f(x))
def sigmoidDerivative(output):
x = sigmoid(output)
return x * ( 1 - x)
Plotando-se o gráfico, obtemos:
No próximo post, será utilizada esta função sigmóide como função de ativação no desenvolvimento e aplicação de uma rede neural Perceptron de múltiplas camadas (Multi Layer Perceptron - MLP) treinada com o algoritmo Back Propagation.
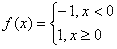

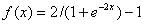



![PythonBrasil[9]](http://2013.pythonbrasil.org.br/divulgue/no-seu-site/pythonbrasil9_en_halfbanner.gif)






ReplyDeletefor preparing bank exam and group exam , we are providing an online test model questions papers
Bank Exam Questions and Answers
Group Exam Questions and Answers
Quando se usa a derivada da sigmoid?
ReplyDeleteAcho que é no backpropagation...quando faz o caminho inverso para corrigir os pesos.
ReplyDeleteAmazing content.
ReplyDeleteData Mining Service Providers in Bangalore
ReplyDeleteThanks for sharingData Mining software service providers
This professional hacker is absolutely reliable and I strongly recommend him for any type of hack you require. I know this because I have hired him severally for various hacks and he has never disappointed me nor any of my friends who have hired him too, he can help you with any of the following hacks:
ReplyDelete-Phone hacks (remotely)
-Credit repair
-Bitcoin recovery (any cryptocurrency)
-Make money from home (USA only)
-Social media hacks
-Website hacks
-Erase criminal records (USA & Canada only)
-Grade change
-funds recovery
Email: onlineghosthacker247@ gmail .com
It is choosing the right one is crucial for efficient gradient propagation, ultimately impacting the model's accuracy and convergence. How Get Better Understanding their dynamics is essential for effective network design.
ReplyDeleteThis is an awesome article, Given such an extraordinary measure of data in it,
ReplyDeleteI feel like I’ve got useful information from your blog.
ReplyDeleteGreat blog. I delighted in perusing your articles
ReplyDeleteExcellent post.I was looking for this certain information for a very long time
ReplyDeleteIt’s so good and so awesome. I am just amazed.
ReplyDeleteIt was definitely informative. This site is useful. Thank you
ReplyDeleteI read this post your post is so nice and very informative post thanks for sharing this post.
ReplyDeleteVery useful and knowledgeable blog.
ReplyDeleteThank you for writing this awesome article.
ReplyDeleteI'm a long time reader but I've never been compelled to leave a comment.
ReplyDeleteI subscribed to your blog and shared this on my Facebook.
ReplyDeleteThanks again for a great article!
ReplyDeleteI have been looking for sites like this for a long time. Thank you!
ReplyDeleteVery value able post, I read the whole story when I start reading it.
ReplyDeleteI needed to see and read this post today and smile.
ReplyDeleteI hope they find each other. simply gorgeous work!
ReplyDelete