3Hi all,
This month I was studying about information retrieval and text mining, specially how to convert the textual representation of information into a Vector Space Model (VSM). The VSM is an algebraic model representing the importance of a term (tf-idf) or even the absence or presence (Bag of Words) of it in a document. I'd like to mention the excellent post from the researcher Christian Perone at his blog Pyevolve about Machine learning and Text Mining with TF-IDF, a great post to read.
I decided in this post to be shorter and give some examples using Python . I expect at the end of this post you feel confortamble to use tf-idf at your tasks handling with text mining.
By the way, I extremely recommend you to check the scikit.learn machine learning toolkit. There is a whole package to work with text classification, including TF-IDF with Python!
What is TF-IDF ?
Term Frequency - Inverse Document Frequency is a weighting scheme that is commonly used in information retrieval tasks. The goal is to model each document into a vector space, ignoring the exact ordering of the words in the document while retaining information about the occurrences of each word.
It is composed by two terms: one first computes the normalized Term Frequency, which is the number of times a word appears in a documnet, divided by the total number of words in that document. Then, the second term is the Inverse Document Frequency, which is computed as the logarithm of the number of the documents in the corpus divided by the number of documents where the term ti appears. Or, in symbols:
and
The TF-IDF gives how important is a word to a document in a collection, since it takes in consideration not only the isolated term but also the term within the document collection. The intuition is that a term that occurs frequently in many documents is not a good discriminator ( why emphasize a term which is almost present in the entire corpus of your documents ?) So it will scale down the frequent terms while scaling up the rare terms; for instance, a term that occurs 10 times more than another isn't 10 times more important thant it.
For computing the TF-IDF weights for each document in the corpus, it is required in the corpus a series of steps: 1) Tokenize the corpus 2) Model the Vector Space and 3) Compute the TF-IDF weight for each document in the corpus.
Tokenization
First we need to tokenize the text. To do this, we can use the NLTK library which is a collection of natural language processing algorithms written in Python. The process of tokenizing the documents in the corpous is a two steps: First the text is splint into sentences, and then the sentences are split into the individual words. It is important to notice that there are several words that are not relevant, that is, terms like "the, is, at, on", etc... aren't going to help us, so in the information extraction, we ignore them. Those words are commonly called stop words and they are present in almost all documents, so it is not relevant for us. In portuguese we also have those stop words such as (a, os , as , os, um , umas, que, etc.)
We will tokenize this collection of documents and represent them as vectors (rows) of a matrix with |D| x F shape, where |D| is the cardinality of the document space, or how many documents we have and the F is the number of features, in our example it is represented by the vocabulary size.
So the matrix representation of our vectors above is:
As you have noticed, these matrices representing the term frequencies (tf) tend to be very sparse (lots of zero-elements), so you will usually see the representation of these matrices as sparse matrices. The code shown below will tokenize each document in the corpus and compute the term frequencies.
Model the Vector Space
Now that each of the documents in the corpus has been tokenized, the next step is to compute the document frequency quantity, that is, for each term, how many documents that term appears in. Before going to IDF, it is important to normalize the term-frequencies. Why ? Imagine that we have a repeated term in document with porpuse of improving its ranking on an Information Retrieval System or even create a bias torwards long documents, making them look more important than they are just because of the high frequency of the term in the document. By normalizing the TF vector we can overcome this problem.
The code.
The code.
Compute the TF-IDF
Now that you saw how the vector normalization was applied, we will now have to compute the second term of tf-idf: the inverse document frequency. The code is provided below:
The TF-IDF is the product between the TF and IDF. So a high weight of the tf-idf is reached when you have a high term frequency (tf) in the given document and low document frequency of the term in the whole collection. Now let's see the tf-idf computed for each term present in the vector space.
The code.
Putting everything together, the following code will compute the TF-IDF weights for each document. And the result matrix it will be:
A row of this matrix would be:
I ommited the zero-values elements of the row.
If we would decide to check the most relevant words for this place, by using the tf-idf I could see that the place has a nice hot chocolate drink (0.420955 <= chocolate quente ótimo), the soft drink nega maluca is also delicious (0.315716 - nega maluca uma delicia), its Cheese bun is also quite good (0.252573 - pao de queijo muito bom).
I ommited the zero-values elements of the row.
If we would decide to check the most relevant words for this place, by using the tf-idf I could see that the place has a nice hot chocolate drink (0.420955 <= chocolate quente ótimo), the soft drink nega maluca is also delicious (0.315716 - nega maluca uma delicia), its Cheese bun is also quite good (0.252573 - pao de queijo muito bom).
And that is how we comput our 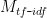 matrix. You can take a look at this link and this one to know how to use it with GenSim and Scikit.Learn respectively.
matrix. You can take a look at this link and this one to know how to use it with GenSim and Scikit.Learn respectively.
That's all, I hope that you enjoyed this article and help more people to know how to implement the tf-idf weight to mine your collection of texts. Feel free to comment and make suggestions.
The source code of this example is also available.
The source code of this example is also available.
Regards,
Marcel Caraciolo





![PythonBrasil[9]](http://2013.pythonbrasil.org.br/divulgue/no-seu-site/pythonbrasil9_en_halfbanner.gif)






Marcelo,thanks a lot for your post. We will use it for teaching the young computer engineers.
ReplyDeletei don't understand why def idf(word, list_of_docs): the variable is named list_of_doc when the variable vocabulary is input?
ReplyDeleteYeah, I was wondering the same thing...
DeleteThanks for this example. Could you reupload 1st and 2nd images. I think those are formulas.
ReplyDeleteNice work
1st and 2nd images are the just the formula for TF and IDF
DeleteThese post were really helpful in understanding the meaning of text mining. It help in putting the unstructured text in a structured form. you can check the website LOGINWORKS http://www.loginworks.com/data-mining/ , to get the accurate data!!
ReplyDeleteEmbedded system training: Wiztech Automation Provides Excellent training in embedded system training in Chennai - IEEE Projects - Mechanical projects in Chennai. Wiztech provide 100% practical training, Individual focus, Free Accommodation, Placement for top companies. The study also includes standard microcontrollers such as Intel 8051, PIC, AVR, ARM, ARMCotex, Arduino, etc.
ReplyDeleteEmbedded system training in chennai
Embedded Course training in chennai
Matlab training in chennai
Android training in chennai
LabVIEW training in chennai
Robotics training in chennai
Oracle training in chennai
Final year projects in chennai
Mechanical projects in chennai
ece projects in chennai
I like the way you start and then conclude your thoughts. Thanks for this nice information.
ReplyDeleteData Analytics Courses in Chennai
Hi admin thanks for sharing informative article on hadoop technology. In coming years, hadoop and big data handling is going to be future of computing world. This field offer huge career prospects for talented professionals. Thus, taking Hadoop & Spark Training in Hyderabad will help you to enter big data hadoop & spark technology.
ReplyDeleteHey how its possible to learn python to assemble machine language through it
ReplyDeleteAndroid training in chennai | Oracle dba Training in Chennai | Python Training in chennai
tf–idf, short for term frequency–inverse document frequency, is a numerical ... PHP Training in Chennai |
ReplyDeletePega Training in Chennai
Máy lạnh âm trần
ReplyDeleteMáy lạnh âm trần Daikin
Máy lạnh âm trần Panasonic
Máy lạnh âm trần Hitachi
Máy lạnh âm trần LG
Máy lạnh Toshiba
Máy lạnh âm trần Mitsubishi Electric
Máy lạnh âm trần Mitsubishi Heavy
Máy lạnh âm trần Reetech
Thanks for sharing this informative blog.
ReplyDeletePython Training in Noida
Python Interview Questions
Python Online Quiz
Machine Learning Tutorial
rem cua
ReplyDeleterèm vải
catalog rèm cửa
rem vai Hàn Quốc
rèm roman
rem cua so
rem van phong
rèm phong tho
rem phong khach
rem phong ngu
rèm phòng cưới
rem phong tre em
mành tre- mành trúc
rèm sáo nhôm
rem la doc
rem cuon
rèm sáo gỗ
phông sân khấu- hội trường
rèm tự động
rèm sợi
rem truong hoc
rem cuon
rem cuon
rèm sáo gỗ
phông sân khấu- hội trường
Useful Post, Thanks for sharing with us
ReplyDeleteBest engineering colleges in jaipur
PHP course is very important nowadays.so learn language quickly & connect a link https://goo.gl/z0JFB7
ReplyDeletehttps://goo.gl/WzKGr2
https://goo.gl/pO7P7J
https://goo.gl/Tshw0J
https://goo.gl/HZJgxn
TestComplete can be act as a backbone of the Web Automation Tool.| https://www.gangboard.com/software-testing-training/test-complete-training
ReplyDeletehttps://www.gangboard.com/crm-training/salesforce-admin-training
https://www.gangboard.com/business-intelligence-training/msbi-training
https://www.gangboard.com/cloud-computing-training/vmware-training
Thank you so much for sharing. it’s useful for me....| Dot Net Training in Annanagar
ReplyDeleteDot Net Training
Thank you for the programs
ReplyDeletePython Training in Chennai
Thank you for explaining the programs on python online training
ReplyDelete#wowwow
ReplyDeleteGreat blog, Thanks..
ReplyDeletelearn arabic online, arabic lessons, learn to speak arabic, arabic learning, online arabic course, online arabic classes, online arabic classes, learn quran, quran teacher, quran for kids,
quran reading, free quran lessons
Thanks for sharing in this blog..
ReplyDeletePLC training in Cochin, Kerala
Automation training in Cochin, Kerala
Embedded System training in Cochin, Kerala
VLSI training in Cochin, Kerala
PLC training institute in Cochin, Kerala
Embedded training in Cochin, Kerala
Best plc training in Cochin, Kerala
It is really a great work and the way in which u r sharing the knowledge is excellent.
ReplyDeleteThanks for helping me to understand basic concepts. As a beginner in dot net programming your post help me a lot.Thanks for your informative article.Dot Net training in chennai | dot net training and placement | Dot Net training in velachery
Thank for you sharing rèm cửa
ReplyDeleteIt is a great thing how well you have created this post, its very unique and informative. This is among the pages that i would bookmark, the information on machine learning with python is quite scary but interesting to read. With a very beautiful Digital Calendar, you will not be required to keep using manual one.Its saves a lot of space, its easy and convenient to use too.
ReplyDeleteBán thuốc diệt kiến của Nhật Bản Super Arinosu Koroki siêu an toàn, diệt 1 con lây chết cả tổ LH 0983131528
ReplyDeletethe blog is about Machine Learning with Python: Meeting TF-IDF for Text Mining it is useful for students and Python Developers for more updates on python follow the link
ReplyDeletePython Online Training
For more info on other technologies go with below links
tableau online training hyderabad
ServiceNow Online Training
mulesoft Online Training
Information is very useful and thanks for sharing
ReplyDeleteNLP Training in Chennai | ramsnlp
Good blog and thanks for sharing this information
ReplyDeleteNLP Certification in Chennai | ramsnlp
Nice Blog Thank You for sharing.python Online Training Hyderabad
ReplyDeleteaem interview questions
ReplyDeletesalesforce interview questions oops abab interview questions
itil interview questions
informatica interview questions extjs interview questions
sap bi interview questions
hive interview questions
seo interview questions
ReplyDeleteas400 interview questions
wordpress interview questions
accounting interview questions
basic accounting and financial interview questions
awesome post nice for sharing...Python Training In Hyderabad!
ReplyDeletePython Training In Ameerpet!
Python Course In Hyderabad!
Try to use the Dịch Vụ Làm Visa Trọn Gói 0983131528 Viseca offers a wide selection of Mastercard and Visa credit cards. Read more online now and make a free comparison.
ReplyDeleteTry to use the Dịch Vụ Làm Visa Trọn Gói Hà Nội 0983.1315.28 Viseca offers a wide selection of Mastercard and Visa credit cards. Read more online now and make a free comparison.
ReplyDeleteGreat post! Thanks for sharing with us.
ReplyDeleteAngularjs Training in Chennai | Web Designing Training in Chennai
the blog is good and Interactive it is about Mulesoft Developer it is useful for students and Mulesoft Developers for more updates on Mulesoft mulesoft Online course hyderabad
ReplyDelete
ReplyDeleteThank you for posting this.
Python Courses in Jaipur
Best Python Training Institutes in Jaipur
Artificial intelligence training in Bangalore
ReplyDeleteMastering Machine Learning
AWS Training in Bangalore
Best Big Data and Hadoop Training in Bangalore
Blockchain training in bangalore
Python Training in Bangalore
This post is much helpful for us. This is really very massive value to all the readers and it will be the only reason for the post to get popular with great authority.
ReplyDeleteBest Online Python training
Great and helpful post and Thanks for sharing this article. we are leading the Best web development & designing, Python, java, android, iPhone, PHP training institute in jodhpur
ReplyDeleteBest Python training and live project training in Jodhpur .
SUPER
ReplyDeletehttp://spunksoft.com/course/rpa-training-in-hyderabad/
Great Article… I love to read your articles because your writing style is too good, its is very very helpful for all of us and I never get bored while reading your article because, they are becomes a more and more interesting from the starting lines until the end.
ReplyDeleteSelenium Training in Bangalore | Selenium Training in Bangalore | Selenium Training in Bangalore | Selenium Training in Bangalore
If someone looking for the best business opportunity in education sector in India. Brainy India is the best option for you.
ReplyDeleteNice tips. Very innovative... Your post shows all your effort and great experience towards your work Your Information is Great if mastered very well.
ReplyDeletepython training in rajajinagar
Python training in bangalore
Python training in usa
Excellent blog, I wish to share your post with my folks circle. It’s really helped me a lot, so keep sharing post like this
ReplyDeleteJava training in Chennai | Java training in Omr
Oracle training in Chennai
Java training in Chennai | Java training in Annanagar
Java training in Chennai | Java training institute in Chennai | Java course in Chennai
Thank you for taking the time to provide us with your valuable information. We strive to provide our candidates with excellent care and we take your comments to heart.As always, we appreciate your confidence and trust in us
ReplyDeleteData Science Training in Chennai | Best Data science Training in Chennai
Data Science training in kalyan nagar
Data science training in Bangalore | Data Science training institute in Bangalore
Data Science training in marathahalli | Data Science training in Bangalore
Data Science interview questions and answers
Data science training in jaya nagar | Data science Training in Bangalore
Very nice article for online training thanks for sharing. Best Python Online Training || Learn Python Course
ReplyDeletenice post..Abacus Classes in chennai
ReplyDeletevedic maths training chennai
abacus training classes in chennai
Low Cost Franchise Opportunities in chennai
education franchise opportunities
franchise opportunities in chennai
ReplyDeleteSome us know all relating to the compelling medium you present powerful steps on this blog and therefore strongly encourage
contribution from other ones on this subject while our own child is truly discovering a great deal.
Have fun with the remaining portion of the year.
Selenium training in bangalore | best selenium training in bangalore | advanced selenium training in bangalore
ReplyDeleteGreetings. I know this is somewhat off-topic, but I was wondering if you knew where I could get a captcha plugin for my comment form? I’m using the same blog platform like yours, and I’m having difficulty finding one? Thanks a lot.
Best AWS Training in Chennai | Amazon Web Services Training Institute in Chennai Velachery, Tambaram, OMR
Advanced AWS Training in Bangalore |Best AWS Training Institute in Bangalore BTMLA ,Marathahalli
I appreciate your efforts because it conveys the message of what you are trying to say. It's a great skill to make even the person who doesn't know about the subject could able to understand the subject . Your blogs are understandable and also elaborately described. I hope to read more and more interesting articles from your blog. All the best.
ReplyDeletemicrosoft azure training in bangalore
rpa training in bangalore
rpa training in pune
best rpa training in bangalore
Superb. I really enjoyed very much with this article here. Really it is an amazing article I had ever read. I hope it will help a lot for all. Thank you so much for this amazing posts and please keep update like this excellent article. thank you for sharing such a great blog with us.
ReplyDeletemicrosoft azure training in bangalore
rpa training in bangalore
rpa training in pune
best rpa training in bangalore
Read all the information that i've given in above article. It'll give u the whole idea about it.
ReplyDeleteBest Devops Training in pune
Devops Training in Bangalore
Power bi training in Chennai
This comment has been removed by the author.
ReplyDeleteI’ve bookmarked your site, and I’m adding your RSS feeds to my Google account.
ReplyDeletepython Online training in chennai
python training institute in marathahalli
python training institute in btm
Python training course in Chennai
Hmm, it seems like your site ate my first comment (it was extremely long) so I guess I’ll just sum it up what I had written and say, I’m thoroughly enjoying your blog. I as well as an aspiring blog writer, but I’m still new to the whole thing. Do you have any recommendations for newbie blog writers? I’d appreciate it.
ReplyDeletepython Online training in chennai
python training institute in marathahalli
python training institute in btm
Python training course in Chennai
Nice information, valuable and excellent design, as share good stuff with good ideas and concepts, lots of great information and inspiration, both of which I need, thanks to offer such a helpful information here.
ReplyDeletepython Course in Pune
python Course institute in Chennai
python Training institute in Bangalore
This is quite educational arrange. It has famous breeding about what I rarity to vouch. Colossal proverb.
ReplyDeleteThis trumpet is a famous tone to nab to troths. Congratulations on a career well achieved.
This arrange is synchronous s informative impolite festivity to pity. I appreciated what you ok extremely here.
Selenium training in bangalore
Selenium training in Chennai
Selenium training in Bangalore
Selenium training in Pune
Selenium Online training
Hii useful blog very good to read
ReplyDeleteblue prism training class in chennai
Very interesting,good job and thanks for sharing such a good blog.your article is so convincing that I never stop myself to say something about it.You’re doing a great job.Keep it up.python training in mumbai
ReplyDelete
,good job and thanks for sharing such a good blog You’re doing a great job.Keep it up !!
ReplyDeletemachine learning training in jaipur
python training in jaipur
best data science training training in jaipur
Hello, I read your blog occasionally, and I own a similar one, and I was just wondering if you get a lot of spam remarks? If so how do you stop it, any plugin or anything you can advise? I get so much lately it’s driving me insane, so any assistance is very much appreciated.
ReplyDeleteAndroid Course Training in Chennai | Best Android Training in Chennai
Datascience Course Training in Chennai | Best Data Science Training in Chennai
Thank you so much for given such an informative blog. Get the best Website Designing and Development Services by Ogeninfo.
ReplyDeleteWebsite Designing Company in Delhi
Good Post. I like your blog. Thanks for Sharing
ReplyDeletePython Training in Noida
ppc company in gurgaon
ReplyDeleteppc company in noida
Get the best performing Mutual Fund by Mutual Fund Wala and know the best investment schemes.
ReplyDeleteMutual Fund Agent
This comment has been removed by the author.
ReplyDeleteAwesome blog again thanks for such an informative blog sharing with us.
ReplyDeleteLifestyle Magazine India
Attend The Python training in bangalore From ExcelR. Practical Python training in bangalore Sessions With Assured Placement Support From Experienced Faculty. ExcelR Offers The Python training in bangalore.
ReplyDeletepython training in bangalore
I have to search sites with relevant information on given topic and provide them to teacher our opinion and the article.
ReplyDeletemachine learning course in bangalore
ReplyDeleteI feel that is among the live casino malaysia so much vital information for me. And i'm satisfied reading your article. However wanna observation on some basic issues, The website taste is great, the articles is in point of fact nice : D. Just right job, cheers The Gaming Club bears a license from the supervision of Gibraltar, and claims to be one of a choose few casinos that have a license from the Gibraltar government. A devotee of the Interactive Gaming Council (IGC), The Gaming Club follows all the guidelines laid the length of by the organization, something that has in imitation of a long way in it mammal certified as a good area to gamble online.
Everything nearly The Gaming Club feels good; be it the promotions, the big number of games, the combined banking options on offer, the highly developed security measures, or the fair and responsible gaming practices the casino adopts.
The Gaming Club motors along upon software developed by one of the giants of online gaming software move on Microgaming. The software it uses is ahead of its time and has a range of features designed to add together your online gambling experience and create you desire to arrive assist after all circular of gambling you accomplish here.
Another hallmark of a fine casino is the quality of its customer withhold team, and The Gaming Club does not disappoint on this front.
http://magnum4dlive.com/
Awesome blog. I enjoyed reading your articles. This is truly a great read for me. I have bookmarked it and I am looking forward to reading Python training in pune new articles. Keep up the good work!
ReplyDeleteNice blog, thank you so much for sharing this informative blog. Visit Ogen Infosystem for the best Website Designing and Development Services in Delhi, India. Also get Digital Marketing Services like PPC, SEO, Social Media Optimization etc.
ReplyDeleteSEO Service in Delhi
Your content is very impressive and thanks for sharing this article. its very useful.
ReplyDeleteReally this is a very useful blog.
sServicenow service portal training
On jobsupport
ReplyDeleteYour content is very impressive and thanks for sharing this article. its very useful.
learn python online
ReplyDeleteYour content is very impressive and thanks for sharing this article. its very useful.
Nice blog, Visit Kalakutir Pvt Ltd for Godown Line Marking Painting, Base Company Logo Painting, and School Bus Painting.
ReplyDeleteSchool Bus Painting
I want to know more about American eagle credit card login
ReplyDeleteThanks for sharing such a great blog Keep posting..
ReplyDeletePython Training in Delhi
Python Course in Delhi
ReplyDeleteExcellent blog, I read your great blog and it is one of the best explanation about this content. Keep doing the new posts...
Pega Training in Chennai
Pega Course
Primavera Training in Chennai
Tableau Training in Chennai
Unix Training in Chennai
Job Openings in Chennai
Placement Training in Chennai
Linux Training in Chennai
JMeter Training in Chennai
Pega Training in T Nagar
Pega Training in Anna Nagar
Nice post..Thanks for sharing...
ReplyDeletePython training in Chennai/
Python training in OMR/
Python training in Velachery/
Python certification training in Chennai/
Python training fees in Chennai/
Python training with placement in Chennai/
Python training in Chennai with Placement/
Python course in Chennai/
Python Certification course in Chennai/
Python online training in Chennai/
Python training in Chennai Quora/
Best Python Training in Chennai/
Best Python training in OMR/
Best Python training in Velachery/
Best Python course in Chennai/
nice article and its very informative...Thanks for sharing...
ReplyDeleteMobile Testing Training in Chennai
Mobile Testing Training
Mobile Application Testing Training
Mobile Testing Training in Velachery
Mobile Testing Training in Tambaram
Manual Testing Training in Chennai
LoadRunner Training in Chennai
Photoshop Classes in Chennai
Spring Training in Chennai
QTP Training in Chennai
Data for a Data Scientist is what Oxygen is to Human Beings. business analytics course with placement this is also a profession where statistical adroit works on data – incepting from Data Collection to Data Cleansing to Data Mining to Statistical Analysis and right through Forecasting, Predictive Modeling and finally Data Optimization.
ReplyDeleteNice blog thank you for sharing
ReplyDeletemachine learning training in bangalore
iot training in bangalore
data science training in bangalore
big data and hadoop training in bangalore
Visit Here=> Best devops training in Bangalore
ReplyDeleteI have seen your blog and really amazing information put in this. If anyone needs Website Designing and Digital Marketing Services in India, visit Ogen Infosystem in Delhi to get a creative and responsive website.
ReplyDeleteBest Website Designing Company in India
VISIT HERE - DEVOPS TRAINING IN BANGALORE
ReplyDeleteClick here to find the Best Big data and Hadoop training in Bangalore
ReplyDeleteAppreciating the persistence you put into your blog and detailed information you provide.
ReplyDeleteCss training in chennai | Css course in chennai
blue prism training in chennai| Blue prism training course in chennai
This concept is a good way to enhance the knowledge.thanks for sharing..
ReplyDeletePython Flask Training
Flask Framework
Python Flask Online Training
Thank you for valuable information.I am privilaged to read this post.microsoft azure training in bangalore
ReplyDeleteVery useful and information content has been shared out here, Thanks for sharing it.google cloud platform training in bangalore
ReplyDeleteThese provided information was really so nice,thanks for giving that post and the more skills to develop after refer that post.blue prism training in bangalore
ReplyDeleteYour articles really impressed for me,because of all information so nice.oracle apps scm training in bangalore
ReplyDeleteinking is very useful thing.you have really helped lots of people who visit blog and provide them use full information.sccm training in bangalore
ReplyDeleteBeing new to the blogging world I feel like there is still so much to learn. Your tips helped to clarify a few things for me as well as giving.vmware training in bangalore
ReplyDeleteReally it was an awesome article,very interesting to read.You have provided an nice article,Thanks for sharing.aws training in bangalore
ReplyDeleteI know that it takes a lot of effort and hard work to write such an informative content like this.data science training in bangalore
ReplyDeleteYour articles really impressed for me,because of all information so nice.robotic process automation (rpa) training in bangalore
ReplyDeleteBeing new to the blogging world I feel like there is still so much to learn. Your tips helped to clarify a few things for me as well as giving.uipath training in bangalore
ReplyDeleteReally it was an awesome article,very interesting to read.You have provided an nice article,Thanks for sharing.blue prism training in bangalore
ReplyDeleteThis is really an awesome post, thanks for it. Keep adding more information to this.openspan training in bangalore
ReplyDeleteI am overwhelmed by your post with such a nice topic. Usually I visit your blogs and get updated through the information you include but today’s blog would be the most appreciable. Well done!
ReplyDeletePlease check ExcelR Data Science Certification
Enjoyed reading the article above, really explains everything in detail, the article is very interesting and effective. Thank you and good luck…
ReplyDeleteStart your journey with Database Developer Training in Bangalore and get hands-on Experience with 100% Placement assistance from experts Trainers @Bangalore Training Academy Located in BTM Layout Bangalore.
That was really a great Article.Thanks for sharing information. Continue doing this.
ReplyDeleteBest SAP EWM Training in Bangalore - Learn from best Real Time Experts Institutes in Bangalore with certified experts & get 100% assistance.
You might comment on the order system of the blog. You should chat it's splendid. Your blog audit would swell up your visitors. I was very pleased to find this site.I wanted to thank you for this great read!!
ReplyDeleteKnow more Data Science Course in Pune
Such a great word which you use in your article and article is amazing knowledge. thank you for sharing it.
ReplyDeleteLearn DevOps from the Industry Experts we bridge the gap between the need of the industry. eTechno Soft Solutions provide the Best DevOps Training in Bangalore .
I am really happy with your blog because your article is very unique and powerful for new reader.
ReplyDeleteaws Training in Bangalore
python Training in Bangalore
hadoop Training in Bangalore
angular js Training in Bangalore
bigdata analytics Training in Bangalore
python Training in Bangalore
aws Training in Bangalore
Such a great information for blogger iam a professional blogger thanks…
ReplyDeleteLearn Best PEGA Training in Bangalore from Experts. Softgen Infotech offers the Best PegaTraining in Bangalore.100% Placement Assistance, Live Classroom Sessions, Only Technical Profiles, 24x7 Lab Infrastructure Support.
A great website with interesting and unique material what else would you need.
ReplyDelete360digitmg Internet ofThings Malaysia
very nice....
ReplyDeleteinplant training in chennai
inplant training in chennai
inplant training in chennai for it.php
namibia web hosting
norway web hosting
rwanda web hosting
spain hosting
turkey web hosting
venezuela hosting
vietnam shared web hosting
very nice....
ReplyDeleteinplant training in chennai
inplant training in chennai
inplant training in chennai for it.php
namibia web hosting
norway web hosting
rwanda web hosting
spain hosting
turkey web hosting
venezuela hosting
vietnam shared web hosting
nice....
ReplyDeleteinternship in chennai for ece students
internships in chennai for cse students 2019
Inplant training in chennai
internship for eee students
free internship in chennai
eee internship in chennai
internship for ece students in chennai
inplant training in bangalore for cse
inplant training in bangalore
ccna training in chennai
Nice Post. Jeewangarg is a Leading Digital Marketing Company which is helping your brand to cut through the Digital Clutter with its best SEO Company in Delhi. Our range of Services includes SEO Services, PPC Services in Delhi, Website Designing Services and Social Media Marketing Services. Being a Google Partners, we provide our client with 100% satisfaction in every aspect of their marketing goals. So, what are you waiting for Connect to the team of best SEO Expert in India, Google Ads Experts, Website Designing Experts, Social Media Experts & more to boost your Digital Presence today with the high quality Digital Marketing Services.
ReplyDeleteThis post is really nice and informative. The explanation given is really comprehensive and informative. devops training videos by 10+ years experienced faculty.
ReplyDeleteSnapdeal Winner List here came up with an Offer where you can win Snapdeal prize list 2020 by just playing a game & win prizes.
ReplyDeleteSnapdeal winner name2020 also check the Snapdeal lucky draw2020
ReplyDeleteThis post is very simple to read and appreciate without leaving any details out. Great work! data science course
ReplyDeleteI am really happy to say it’s an interesting post to read . I learn new information from your article , you are doing a great job . Keep it up and a i also want to share some information regarding selenium testing course and selenium training videos
Nice post..intersting info
ReplyDeleteArtificial intelligence course hyderabad
Thank you for your post. This is excellent information. It is amazing and wonderful to visit your site.
ReplyDeleteaws Training in Bangalore
python Training in Bangalore
hadoop Training in Bangalore
angular js Training in Bangalore
bigdata analytics Training in Bangalore
python Training in Bangalore
aws Training in Bangalore
Thanks for sharing such a great information. Its really nice and informative learn ai programming.
ReplyDeleteI seriously love your site.. Excellent colors & theme. Did you develop this web site yourself? Please reply back as I’m looking to create my own blog and want to know where you got this from or just what the website theme is called. Thank you!
ReplyDeleteGood Post.Thanks for Sharing
ReplyDeletewebsite designing company in Delhi
Enjoyed reading this article throughout.Nice post! IoT is the trendy course right now and is going to be in
ReplyDeletea great demand in near future as jobs for this domain will be sky rocketted.To be on par with the current trend we have to
gain complete knowledge about the subject. For the complete course online
360Digitmg Iot Certification Training
360Digitmg Internet of things courses online
Hi, Thanks for sharing wonderful stuff...
ReplyDeleteFor More:
Data Science Training In Hyderabad
I really enjoy By reading of all your Articles. Simply wanted to inform you that you have people like me who appreciate your work. Definitely a great post. The information that you have provided is very helpful for me.
ReplyDeleteMachine Learning Training In Hyderabad
Nice article. For offshore hiring services visit:
ReplyDeleterenaissancetainela
Thanks for the informative article About AWS. This is one of the best resources I have found in quite some time. Nicely written and great info. I really cannot thank you enough for sharing.
ReplyDeleteJava training in chennai | Java training in annanagar | Java training in omr | Java training in porur | Java training in tambaram | Java training in velachery
Excellent Blog ..Thanks for sharing...
ReplyDeletePython Course Training in chennai | Data Science Course Training in chennai | Best Data Science Training Institute in chennai | Machine Learning Course Training in chennai | RPA Course Training in chennai | RPA Training Institute in chennai | Best AWS Training Institute in chennai | DevOps Course Training in chennai | Best DevOps Training Institute in chennai | AWS Course Training in chennai | Best Java Training Institute in chennai | Java Training in chennai | Selenium Course Training in chennai | Best Selenium Training Institute in chennai | Java Course Training in chennai | Dot Net Course Training in chennai | Dot Net Training Institute in chennai
nice blog about machine lerning & phython information you provide very helpful information.
ReplyDeleteair hostess institute
All the contents you mentioned in post is too good and can be very useful. I will keep it in mind, thanks for sharing the information keep updating, looking forward for more posts.Thanks
ReplyDeleteData Science Course in Bangalore
This is my first time i visit here and I found so many interesting stuff in your blog especially it's discussion, thank you.
ReplyDeleteData Science Training in Bangalore
python training in bangalore | python onloine training
ReplyDeletethanks for sharing this post!
ReplyDeleteI really like it!
đại lý bán máy lạnh giá sỉ
máy lạnh âm trần daikin
máy lạnh tủ đứng daikin
máy lạnh giấu trần nối ống gió daikin
máy lạnh multi daikin
I just stumbled upon your blog and wanted to say that I have really enjoyed reading your blog posts. Awesome blog. I enjoyed reading your articles. This is truly a great read for me. I have bookmarked it and I am looking forward to reading new articles. Keep up the good work!.
ReplyDeleteData Science Course in Bangalore
Data Science Training in Bangalore
PMP Certification Training in Hyderabad
Data Science Training in Pune
Data Science Course in Pune
python training in bangalore | python online taining
ReplyDeleteaws training in bangalore | aws online training
artificial intelligence training in bangalore | artificial intelligence online training
machine learning training in bangalore | machine learning online training
data science training in bangalore | data science online training
Analytics certification is an area of study in the world of data analytics which addresses the process of decision-making using data analysis. machine learning course hyderabad
ReplyDeletereally great.
ReplyDeletePHP Training in Chennai | Certification | Online Training Course | Machine Learning Training in Chennai | Certification | Online Training Course | iOT Training in Chennai | Certification | Online Training Course | Blockchain Training in Chennai | Certification | Online Training Course | Open Stack Training in Chennai |
Certification | Online Training Course
Excellent post. Useful resource. Thank you for sharing with us.
ReplyDeleteAWS training in Chennai
AWS Online Training in Chennai
AWS training in Bangalore
AWS training in Hyderabad
AWS training in Coimbatore
AWS training
Great Article
ReplyDeleteFinal Year Projects in Python
Python Training in Chennai
FInal Year Project Centers in Chennai
Python Training in Chennai
A great website with interesting and unique material what else would you need.data science course
ReplyDeleteIf you don"t mind proceed with this extraordinary work and I anticipate a greater amount of your magnificent blog entriesdata science certification
ReplyDeleteMmm.. good to be here in your article or post, whatever, I think I should also work hard for my own website like I see some good and updated working in your site.data science course in delhi
ReplyDeleteHire Magento Developer in Kochi
ReplyDeletePhp Internship in Kochi
IT Consulting Services in Kochi
ReplyDeleteexcellent way of writing
Data science Training in bangalore
Aws Training In Bangalore
Hadoop Training In Bangalore
Devops Training In Bangalore
Iot Training in Bangalore
Really nice and interesting post. I was looking for this kind of information and enjoyed reading this one. Keep posting. Thanks for sharing.
ReplyDeleteSimple Linear Regression
Correlation vs covariance
KNN Algorithm
This Was An Amazing ! I Haven't Seen This Type of Blog Ever ! Thankyou For Sharing, data scientist course in hyderabad with placement
ReplyDeleteThanks for Sharing This Article.It is very so much valuable content. I hope these Commenting lists will help to my website
ReplyDeletepython training in bangalore
python training in hyderabad
python online training
python training
python flask training
python flask online training
python training in coimbatore
very special. easy to understand…. taking things from root .. stay blessed machine learning online course!
ReplyDeleteMachine Learning Courses in Pune I really enjoy reading and also appreciate your work. I read that Post and got it fine and informative. Please share more like that...
ReplyDeleteI have bookmarked your website because this site contains valuable information in it. I am really happy with articles quality and presentation. Thanks a lot for keeping great stuff. I am very much thankful for this site.
<a href="https://www.excelr.com/business-analytics-training-in-pune/”> Business Analytics Courses </a>
ReplyDeleteI am always searching online for articles that can help me. There is obviously a lot to know about this. I think you made some good points in Features also. Keep working, great job !
This professional hacker is absolutely reliable and I strongly recommend him for any type of hack you require. I know this because I have hired him severally for various hacks and he has never disappointed me nor any of my friends who have hired him too, he can help you with any of the following hacks:
ReplyDelete-Phone hacks (remotely)
-Credit repair
-Bitcoin recovery (any cryptocurrency)
-Make money from home (USA only)
-Social media hacks
-Website hacks
-Erase criminal records (USA & Canada only)
-Grade change
-funds recovery
Email: onlineghosthacker247@ gmail .com
This professional hacker is absolutely reliable and I strongly recommend him for any type of hack you require. I know this because I have hired him severally for various hacks and he has never disappointed me nor any of my friends who have hired him too, he can help you with any of the following hacks:
ReplyDelete-Phone hacks (remotely)
-Credit repair
-Bitcoin recovery (any cryptocurrency)
-Make money from home (USA only)
-Social media hacks
-Website hacks
-Erase criminal records (USA & Canada only)
-Grade change
-funds recovery
Email: onlineghosthacker247@ gmail .com
<a href="https://www.excelr.com/business-analytics-training-in-pune/”> Courses in Business Analytics</a> have express a few of the articles on your website now, and I really like your style of blogging. I added it to my favorite’s blog site list and will be checking back soon…
ReplyDeleteI am always searching online for articles that can help me. There is obviously a lot to know about this. I think you made some good points in Features also. Keep working, great job !
Looking for JOB in core industry? We're offering additional discount on early enrollment on full module Automation Training. Certificate will be given to those who completed their training and also get 100% Job assistance(Life Time).Call 9953489987, 9711287737.
ReplyDeleteIt's really a good blog kindly thank you for sharing this.
ReplyDelete3D Scanning Services Near Me
The article is very interesting and effective.
ReplyDeletePYthon Training in Gurgaon
Easily, the article is actually the best topic on this registry related issue. I fit in with your conclusions and will eagerly look forward to your next updates. Just saying thanks will not just be sufficient, for the fantasti c lucidity in your writing. I will instantly grab your rss feed to stay informed of any updates.
ReplyDeleteData Science Training
I am really happy with your blog because your article is very unique and powerful for new reader.
ReplyDeleteDevOps Training in Chennai
DevOps Course in Chennai
PYTHON ONLINE TRAINING || PYTHON ONLINE Course
ReplyDeleteI really thank you for the valuable info on this great subject and look forward to more great posts ExcelR Business Analytics Courses
ReplyDeleteI read that Post and got it fine and informative. Please share more like that...
ReplyDeletedata science in malaysia
Machine Learning Training in Noida
ReplyDeleteThanks for this valuable information!
ReplyDeleteData Science Online Training
Python Online Training
Salesforce Online Training
Thank you for sharing this amazing blog.
ReplyDeleteThanks a lot.
I want to share infographic of applications of Machine Learning
You can also hire AI and Machine Learning Developers from Dark Bears.
The writer is enthusiastic about purchasing wooden furniture on the web and his exploration about best wooden furniture has brought about the arrangement of this article. ExcelR Data Analyst Course
ReplyDeleteThis Blog is very useful and informative.
ReplyDeleteai course in noida
Mua vé tại Aivivu, tham khảo
ReplyDeletegiá vé máy bay đi Mỹ khứ hồi
vé máy bay hải phòng sài gòn
vé bay đà lạt hà nội
vé máy bay giá rẻ đi Huế
vé máy bay đi qui nhơn
thuê xe ra sân bay nội bài
combo vinpearl phú quốc 3 ngày 2 đêm 2021
Thanks for the information about Blogspot very informative for everyone
ReplyDeletedata scientist course
I cannot thank you enough for the blog.Thanks Again. Keep writing.
ReplyDeletedata science training
python training
angular js training
selenium trainings
sql server dba training
Very amazing and interesting post, thank you for sharing
ReplyDeleteData Science Training In Pune
Looking for the best online Arabic Classes in Malaysia? Join Ziyyara as we have the best selected online Arabic tutors for you in Malaysia.
ReplyDeleteContact no:- @9654271931
Visit On:- Online Arabic Class in Malaysia
nicepost.
ReplyDeleteazure online training
azure training
ReplyDeleteI love to have this kind of information. www.hairsalonmarinadelrey.com
cơ hội đầu tư cho bạn tại Big Đầu tư
ReplyDeleteJoin now and be the first to enjoy the advantages that come with Artificial Intelligence Training in Hyderabad and build your career in the field of Artificial Intelligence by joining AI Patasala.
ReplyDeleteArtificial Intelligence Training Hyderabad
Studyprovider has experts team are giving the homework help, assignment help, report, thesis, research writing services and lab report assignment help available 24/7 seven days a week contact now.
ReplyDeleteThanks for sharing valuable information..
ReplyDeleteGreat post.Keep posting great article like this with us.
HSC Training in kerala|Safety Courses In Kerala
I want you to thank for your time of this wonderful read!!! I definately enjoy every little bit of it and I have you bookmarked to check out new stuff of your blog a must read blog!
ReplyDeletedata scientist certification malaysia
Nice blog! Thanks for sharing this valuable information
ReplyDeleteRPA Training in Hyderabad
RPA Training in Gurgaon
This is really an amazing article. Your article is really good and your article has always good content with a good powerpoint with informative information.
ReplyDeleteBest Hospital in Jaipur
cardiology hospital in Jaipur
Super speciality hospital in Jaipur
asthma and Allergy hospital in Jaipur
endocrinology hospital in Jaipur
Neurology hospital in Jaipur
Your blog provided us with valuable information to work with. Each & every tips of your post are awesome. Thanks a lot for sharing. Keep blogging,
ReplyDeletedata scientist course in hyderabad
Great article, thank you for sharing.
ReplyDeleteRPA Training
Thank you the sharing the most informative blog for us. It may helpfull for you all.
ReplyDeleteJava Training in Chennai
Java Training Institute in Chennai
Thanks for sharing this information. Machine Learning Course in Pune
ReplyDeletevery useful and informative blog.
ReplyDeleteartificial intelligence Classes in Pune
nice post. Full Stack Course In Amravati
ReplyDeleteAnkara
ReplyDeleteBolu
Sakarya
Mersin
Malatya
DTWU
adıyaman
ReplyDeletesakarya
yalova
tekirdağ
amasya
JWX6
Nice blog Post. Thanks for posting.
ReplyDeleteVisit Python Classes in Pune
Azure DevOps Training Online
ReplyDeleteAzure DevOps Online Training
Azure DevOps Training in Ameerpet
Snowflake Training
Snowflake Training in Hyderabad
Artificial Intelligence Courses Online
Artificial Intelligence Training in Hyderabad
Microsoft Fabric Training
Microsoft Azure Fabric Training
etgryhgtrhujt
ReplyDeleteكشف تسربات المياه بالاحساء
Great post! Really appreciate the clear explanation of TF-IDF and the detailed Python examples. Super helpful for anyone diving into text mining. Keep up the awesome work!
ReplyDeletecyber security internship for freshers | cyber security internship in chennai | ethical hacking internship | cloud computing internship | aws internship | ccna course in chennai | java internship online
This blog provide the more information. Thank you so much for sharing with us.
ReplyDeletePython Training in Bangalore
شركة عزل خزانات بالرس TbaI3EHMGY
ReplyDeleteشركة تسليك مجاري بالقطيف UcuoIwEsgz
ReplyDeleteI appreciate the inclusion of best practices for data cleaning and preprocessing in this article...... data analyst internship in Chennai
ReplyDeleteNice blog Post. Thanks for posting.
ReplyDeleteupcoming Residential Project in Hyderabad