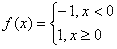Olá a todos,
Nesse primeiro artigo, estarei escrevendo sobre as Redes Neurais e algumas implementações simples desenvolvidas em Python.
Apresentando as Redes Neurais
O que são? - “São sistemas de processamento de sinais ou de informações, compostos por um grande número de processadores elementares chamados neurônios artificiais, operando de forma paralela e distribuída, de modo a resolver um determinado problema físico/computacional.”
Esquema! - (X1, X2, …, Xn) * (W1, W2, …, Wn) — F(x) — Y
Isso significa que uma Rede Neural, de um neurônio apenas, é um combinador linear que passa por uma função de ativação e dá um resultado Y, o mais interessante é que podemos programá-la para que ela dê o resultado que você deseje!
Com isso podemos fazer, dentre outras coisas, aproximadores de funções, associadores, classificação de padrões, predição futura, controle de sistemas, filtragem de sinais, compressão de dados, datamining, etc.
Redes Neurais podem ser de vários tipos, nesta parte básica vamos ver as mais simples, as Redes Neurais supervisionadas, que são treinadas (ou programadas) usando um conjunto de exemplos conhecidos, com atributos e respostas, e desta forma a Rede Neural “se acostuma” em dar os resultados desejados e passa a responder de acordo.
Programar uma Rede Neural é ajustar os valores do vetor W, de todos os neurônios, para que determinada entrada X, quando processada, resulte num valor Y desejado.
Eu irei começar com a mais simples redes neurais de todas, a Perceptron com apenas uma camada de neurônios e trabalhar sobre as diferentes arquiteturas e técnicas de aprendizado que eventualmente irão convergir para redes que podem prever tendências dos preços das ações de uma bolsa de valores, reconhecimento de padrões, processamento de linguagem natural, etc.
O Perceptron é o ancião de todas as redes neurais. Ela foi criada em 1957 nos laboratórios das forças militares por Frank Rosenblatt. O Perceptron é o mais simples tipo de rede neural diretas (Feedfoward) , conhecido como classificador linear. Isto significa que os tipos de problemas solucionados por esta rede neural devem ser linearmente separáveis. O que significa isso ? O gráfico abaixo ilustra facilmente o que ser um problema linearmente/não-linearmente separáveis em duas dimensões.
 |  |
| Lineamente Separável. | Não linearmente separável. |
A linha verde representa a separação entre duas classes de dados que uma rede está tentando classificar. Em três dimensões, isto seria representado por um plano, e em 4 dimensões ou mais por um hiper-plano. Há outros tipos de redes de neurais que pdoem solucionar problemas linearmente e não linearmente separáveis, que serão discutidas em futuros posts.
Para tentar resolver este problema, nós precisamos de uma rede representada pela figura abaixo.
Como vocês podem observar, cada nó de entrada (input) está diretamente conectado ao nó de saída (output). Ajustando os valores dos pesos (weight) que conectam tais nós , a rede é capaz de aprender.
Em uma simples demonstração, irei usar o conjunto de dados plotados no primeiro gráfico aqui apresentado como os dados de treinamento (conjunto de dados para treinamento). O conjunto de dados de treinamento será usado repetidamente como entrada para os nós de entrada (input) da rede neural, fazendo com que os pesos se ajustem até a rede neural atinja o desempenho e objetivo desejado, que é classificar um conjunto de dados linearmente separáveis.
Uma vez que a rede neural foi treinada, a aplicação irá acessar uma base de dados (diferente dos dados de treinamento) e irá provar que a rede neural aprendeu corretamente e tem a capacidade de generalização; ela pode encontrar respostas corretas mesmos quandos os dados de entrada estão incompletos ou quando a relação entre a entrada e a saída não é concreta.
O código abaixo mostra como isso foi realizado.
Um algoritmo simples
Este descreve apenas o funcionamento de um neurônio.
##################################################
# #
# Copyright 2008 Marcel Pinheiro Caraciolo #
# #
# #
# -- Perceptron Neural Net snippet code #
# -- Version: 0.1 - 12/12/2008 #
##################################################
#Snippet Neuron
from random import random
class Neuron:
def __init__(self,data,learningRate = 0.1):
self._learning_rate = learningRate
self._input,self._output = data
#Randomise weights.
self._weight = map(lambda x: x*random(), [1] * len(self._input))
#print self._weight
self._y = None
self._global_error = 0.0
def train(self,data):
self._input,self._output = data
#Calculate output.
self._y = self._sign(self._sum())
#Calculate error.
if self._error() != 0:
#Update weights.
self._adjustWeight()
#Convert error to absolute value.
self._global_error += abs(self._error())
def execute(self,input):
self._input = input
#Calculate output.
self._y = self._sign(self._sum())
return self._y
def _sum(self):
return sum(map(lambda x,y: x*y, self._input,self._weight))
def _sign(self,output):
if output < 0:
y = -1
else:
y = 1
return y
def _error(self):
return self._output - self._y
def _adjustWeight(self):
self._weight = map(lambda x,y: x + (y*self._learning_rate*self._error()),self._weight,self._input)
def getGlobalError(self):
return self._global_error
def resetGlobalError(self):
self._global_error = 0
E para executar o perceptron, que é o que irá apresentar os exemplos ao neurônio, temos:
##################################################
# #
# Copyright 2008 -Marcel Pinheiro Caraciolo- #
# #
# #
# -- Perceptron Neural Net snippet code #
# -- Version: 0.1 - 12/12/2008 #
##################################################
#Snippet Perceptron
from Neuron import *
class Perceptron:
def __init__(self,inputs,iterations=100):
self._inputs = inputs
self._refresh_inputs = list(inputs)
self._iterations = iterations
self._iteration = 0
self._neuron = Neuron(self._getRandInput())
self._train()
def _train(self):
while self._iteration <= self._iterations:
self._neuron.resetGlobalError()
self._refresh_inputs = list(self._inputs)
for i in range(len(self._refresh_inputs)):
self._neuron.train(self._getRandInput())
print "Iteration %d Error: %f" % (self._iteration, self._neuron.getGlobalError())
self._iteration += 1
if(self._neuron.getGlobalError() == 0.0):
break
def _getRandInput(self):
return self._refresh_inputs.pop()
def execute(self,input):
return self._neuron.execute(input)
def arange(self,start,stop=None,step=None):
if stop is None:
stop = float(start)
start = 0.0
if step is None:
step = 1.0
cur = float(start)
while cur <= stop:
yield cur
cur+=step
Execute as classes acima usando:
#main Logic
#Load sample input patterns
inputs = [ [[0.72, 0.82], -1], [[0.91, -0.69], -1],
[[0.46, 0.80], -1], [[0.03, 0.93], -1],
[[0.12, 0.25], -1], [[0.96, 0.47], -1],
[[0.8, -0.75], -1], [[0.46, 0.98], -1],
[[0.66, 0.24], -1], [[0.72, -0.15], -1],
[[0.35, 0.01], -1], [[-0.16, 0.84], -1],
[[-0.04, 0.68], -1], [[-0.11, 0.1], 1],
[[0.31, -0.96], 1], [[0.0, -0.26], 1],
[[-0.43, -0.65], 1], [[0.57, -0.97], 1],
[[-0.47, -0.03], 1], [[-0.72, -0.64], 1],
[[-0.57, 0.15], 1], [[-0.25, -0.43], 1],
[[0.47, -0.88], 1], [[-0.12, -0.9], 1],
[[-0.58, 0.62], 1], [[-0.48, 0.05], 1],
[[-0.79, -0.92], 1], [[-0.42, -0.09], 1],
[[-0.76, 0.65], 1], [[-0.77, -0.76], 1]]
perceptron = Perceptron(inputs,1000)
#Display network generalization
print ""
print "X, Y, Output"
for i in perceptron.arange(-1,1,0.5):
for j in perceptron.arange(-1,1,0.5):
#Calculate output.
result = perceptron.execute(list((i,j)))
if result == 1:
result = "Blue"
else:
result = "Red"
print "%f %f %s" % (i,j,result)
A saída da rede após o treinamento é exibida conforme abaixo, o que prova que a generalização foi atingida. Cada par de coordenadas (x,y) quando apresentadas à rede, retorna a classificação esperada, isto é, vermelho ou azul.
(...)
X, Y, Output
-1.000000 -1.000000 Blue
-1.000000 -0.500000 Blue
-1.000000 0.000000 Blue
-1.000000 0.500000 Blue
-1.000000 1.000000 Blue
-0.500000 -1.000000 Blue
-0.500000 -0.500000 Blue
-0.500000 0.000000 Blue
-0.500000 0.500000 Blue
-0.500000 1.000000 Red
0.000000 -1.000000 Blue
0.000000 -0.500000 Blue
0.000000 0.000000 Blue
0.000000 0.500000 Red
0.000000 1.000000 Red
0.500000 -1.000000 Blue
0.500000 -0.500000 Red
0.500000 0.000000 Red
0.500000 0.500000 Red
0.500000 1.000000 Red
1.000000 -1.000000 Red
1.000000 -0.500000 Red
1.000000 0.000000 Red
1.000000 0.500000 Red
1.000000 1.000000 Red
Analise o objeto criado, seus métodos e pesos, verifique que com o método “execute” você poderá testar se as respostas estão sendo dadas corretamente.
Além de problemas triviais como este de classificação de 2 dimensões , o Perceptron pode realizar uma análise mais poderosa em mais dimensões. As regras genéricas aqui apresentadas são também aplicáveis.
No próximo post, eu falarei mais sobre a Adaline, que é outro tipo de rede neural feedfoward como o Perceptron.
Download dos códigos aqui.
![PythonBrasil[9]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_tP4Z3Rubk_SKcig_7u4Fw_rcrejdgwMeCL-SANVKnNnGouaLjsZ3BU6W0q3Yvo0GX5cmZN68RbzX0DLwxNObMuuvo6fZ4_AJr7Amovo0ok8bqCPCkd90Pnj5sHEi7Tpeu4GHLQEmfPUzdS19RGwTtrFBFOt0Xi4Q=s0-d)
Posts
